旋轉光學尺的精度

旋轉（角度*）光學尺可用在各種各樣的機器和設備上。旋轉光學尺由一個位置量測讀頭和一個刻在旋轉光學尺柱面或碟盤表面的精確柵尺組成。讀頭通過光學方式感應間隔規則的刻度標記來量測位置，並以類比或數位訊號的形式輸出這些資訊。隨後，訊號通過數顯表 (DRO) 或運動控制器轉換為位置讀數。本白皮書簡述影響旋轉（角度）光學尺效能的主要因素，協助設計人員為其選擇的應用領域選擇最佳光學尺系統。

*角度光學尺一般具有 10,000 或以上的刻線數，精度優於 ±5 角秒。嚴格來說，「旋轉光學尺」是指低於這些標準的光學尺，但通常用作描述所有圓形光學尺的通用術語。

許多現代自動化系統都需要精密的旋轉運動，如旋轉式電腦直接製版 (CTP) 預壓機，工具機 A、B 和 C 軸、表面黏著機、形狀量測系統、晶圓處理和檢測設備以及測角儀。不同的應用需要不同的光學尺效能和特性組合，以優化其功能 — 有些對精度有要求，有些則要求重複性、高解析度或低週期誤差，以實現速度迴路控制。選擇能夠在技術規格和功能之間實現最佳平衡的光學尺極具挑戰性，很少有光學尺能夠滿足所有的要求。

精密運動控制取決於系統的精度和動態響應。準確量測位置固然重要，但如果不能精確控制位置，系統也無法正常工作。直驅旋轉馬達（或稱扭矩馬達）具備高扭矩，可在非常小的角度範圍內實現精密伺服控制。由於負載直接耦合至驅動馬達，無需安裝會引起反向間隙、滯後、齒輪誤差或皮帶拉伸等狀況的傳動部件，所以其動態回應極佳。雖然大內徑扭矩馬達的無框架結構沒有明顯可用的聯軸器來安裝軸式光學尺，但旋轉光學尺可提供簡便的解決方案。此外，旋轉光學尺可以像負載一樣剛性耦合至驅動馬達，消除了系統中不必要的間隙。在任何量測或控制系統中，光學尺最好盡可能接近驅動馬達，這有助於將影響伺服效能的潛在軸共振降至最低，特別是在伺服頻寬增加時。

圖 1.安裝在直驅馬達（SOLPOWER，台灣）上的 Renishaw RESOLUTE™ RESA 旋轉光學尺。

旋轉光學尺是提供精密角度位置回饋的優良解決方案。與選擇馬達一樣，要選擇正確的旋轉光學尺，應根據實際的規格要求，瞭解影響光學尺精度的因素，並充分瞭解如何克服效能短板。在選擇旋轉光學尺時，明智的做法是除了考慮精度和解析度外，還要考慮資料速率、系統大小、複雜性和成本等一系列參數。如今線性光學尺的量測精度和解析度可達到幾十奈米，而旋轉光學尺的量測效能可達到一角秒以內。

一角秒是一個很小的角度：

可表示為半徑 206.25 mm 時，弧長 1 微米對應的角度。
可表示為地表上 30 m 距離與地心對應的夾角。
可解析為 1 轉/秒時 1.3 MHz 的資料速率。

在確定所需的量測效能時，考慮精度、解析度和重複性非常有用：

對於重複性要求高的應用（例如打件機），系統反復在相同的光學尺計數位置停止運動比各工作台角度的精確性更重要。
對於連續平穩運動，所選的光學尺解析度和精度不允許在控制伺服頻寬內發生抖動誤差。
對於慢速移動的裝置，例如天文望遠鏡，精確的角度量測比系統最高資料速率更重要。
對於高速系統，可能需要在速度和定位精度之間取捨；粗柵距（刻線數較少）光學尺適合高資料速率，但細柵距（刻線數較多）光學尺通常具有較低的細分誤差。

瞭解系統的精度要求後，再選擇合適的光學尺就容易多了。儘管某些廠商這樣聲稱，但「隨插即用」的方式極少能實現高精度旋轉量測 — 瞭解誤差預算對於優化效能至關重要。雖然本白皮書參照的是圖 3 所示的旋轉光學尺，但同樣的參數也適用於圖 2 所示的 Renishaw RCDM 光學尺碟盤等表面讀取型旋轉光學尺。

圖 2.RCDM 碟盤上的 ATOM™ 光學尺讀頭。

圖 3.DDR 轉台應用，帶原位 RESOLUTE 絕對式光學尺（ITRI，台灣）。

建立誤差預算

想像一下，兒童在學校用塑膠量角器在紙上量測兩條線之間的夾角。他們把量角器直接放在紙上，讓量角器的底線直接壓住其中一條線，並調整其位置，直到原點與兩條線的交點重合。然後在刻度尺上讀出兩條線之間的夾角，必要時進行細分以滿足所需的解析度。開始的幾次，他們的讀數可能與老師的讀數不同，老師需要強調將量角器準確居中並對齊線性的重要性。這些校準誤差對測得角度的影響可能比塑膠量角器自身角度刻度不規則對結果的影響更大。

孩子們已經學會了準確量測角度的三條規則：

盡可能將圓尺的中心對準被測角的頂點。
使測尺盡可能接近被測項目。
儘量減少測尺與被測項目之間的相對（角度）運動。

還有其他三個因素可能沒有考慮到：

整個圓周上刻度間的圓周距離應一致。
對於所有角度位置，徑向刻度中心與進行量測的刻度尺邊緣之間的徑向距離應相同。
量測角度時，應通過量角器垂直觀察線性，儘量減少視差。

與在紙上使用塑膠量角器一樣，這些先決條件同樣適用於機器中的旋轉光學尺。

圖 5 中，要量測或控制其角度運動的待測部件在一根軸上旋轉，而這根軸安裝於兩個軸承上。帶有內建軸承的旋轉光學尺耦合至該軸，並通過安裝在非旋轉結構上的讀頭讀取。鑒於上述規則，要使光學尺系統輸出反映待測部件的實際旋轉運動，必須符合以下要求：

系統的每個部分在其軸承上旋轉時必須無相對於旋轉軸的徑向跳動（即側向運動）。
連接待測部件與光學尺的軸系統在扭矩作用下應具有剛性。
聯軸器的設計應使光學尺在其軸承內旋轉的角度運動與在其自身軸承系統內旋轉的待測部件的角度運動相同；即需要一個等速接頭。
柵尺邊緣周圍的各條刻線之間的間隔應該一致，讀頭應該以線性方式對刻線進行細分。
柵尺應該是真正的圓形，其旋轉軸應垂直穿過圓心。
讀頭讀取柵尺時應無視差或其他幾何誤差，而且必須牢牢固定在非旋轉參考框架上。

如果以上任何一個條件不能得到滿足，待測部件的角度位置與光學尺系統所報告的角度位置之間將出現偏差。通過研究每一個可能的誤差源，可以確定各個誤差源所引起的誤差大小，從而確定整個系統的總誤差預算。

軸承跳動效應

「軸承跳動」一詞用來描述引起部件和/或光學尺的旋轉軸發生徑向跳動（或側向平移）的各種系統屬性。徑向跳動包括由軸承系統缺陷造成的可重複分量和不可重複分量：包括間隙、高次諧波（如球和滾道缺陷）和偏心（見圖 4）。

在滾動軸承上運轉的主軸徑向跳動幅度受軸承系統的設計和調整影響，但通常超過 ±1 µm。由於光學尺系統對其圓尺的圓周位置的解析度至少能達到該值的十分之一，由此可以看到，軸承跳動引起的誤差可覆蓋精良設計的系統的其餘部分引起的誤差。軸承跳動的誤差因素表示為：

角度量測誤差（角秒）= 軸承跳動 (μm) x 412.5/D其中 D 是柵尺的直徑，單位為 mm。

儘管表現出週期分量，但由於任何用於補償的誤差補正都必須補正許多主軸轉數，因此該量測誤差可能很難評估。

對於高精度系統，由於選擇正確的軸承徑向剛度可以將徑向跳動降至亞微米級，因此最好使用設計精良的空氣軸承。使用空氣軸承時，必須考慮失衡力的影響：低速條件下，主軸繞其幾何中心線旋轉，但在高速條件下，當失衡向心反作用力超過軸承及其安裝件的徑向剛度時，主軸繞其質心旋轉。雖然這種轉變通常在高速條件下發生，但在靜態和動態中心線之間可能出現幾個微米的差異。此徑向跳動可重複，因此可以按主軸每旋轉一周出現一個週期進行預測。

無論使用哪種軸承，都應注意以下事項：

對於圖 5 所示系統，只有支撐光學尺的軸承會產生軸承跳動誤差。然而，其所產生的優勢可能被聯軸器引起的其他誤差削弱。
儘管有消除軸承跳動效應的技術（特別是在同一個柵尺上使用兩個或多個讀頭），但必須考慮角度量測的目的：
- 例如，使用經緯儀量測水平或垂直平面上各點之間的角間距時，即使是明顯的軸承跳動，也可以用兩個讀頭來補償。
- 如果需要位置回饋以使用極座標來定位旋轉元件上的給定點（如晶圓檢測機應用），除非在同一個旋轉光學尺上使用三個或更多讀頭，否則支撐待測部件的軸承的任何軸向跳動都將影響定位精度。

如果不可避免地會產生較大的軸承跳動，則必須考慮選擇適當的柵距。根據經驗法則，如果增量訊號是 2 個或多個讀頭的平均值（參考零位元來自其中一個讀頭），則柵距應超出軸承跳動 3 到 4 倍，如果小於這個值，參考零位重複性方面的問題可能會很嚴重，除非採用補償技術，如 Renishaw 的 propoZ™ 技術。

耦合誤差效應

圖 5 所示系統含有一個獨立的旋轉光學尺，其軸承通過一個聯軸器連接到待測部件。這種設計的優點是，只有光學尺軸承的跳動會影響角度量測精度。然而，如果系統要返回待測部件上某一點的極座標，而非遠處某個物體的角度軸承上的點，則主軸承的跳動將影響定位精度，因此我們必須謹慎看待這一「優點」。

聯軸器本身的設計也可能對系統精度產生顯著影響。

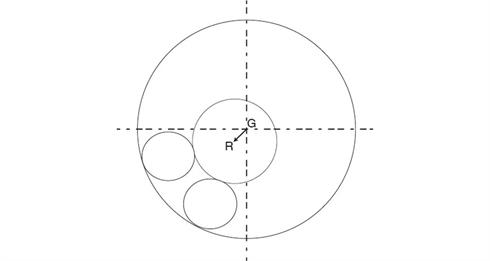
圖 4.軸承跳動是總偏心度的構成因素之一，是旋轉軸 (R) 從幾何中心 (G) 開始的位移。

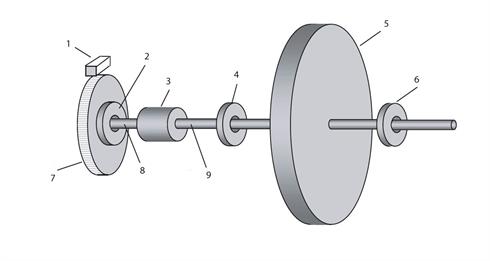
圖 5.通用機器系統。1) 讀頭 2) 光學尺軸承

3) 聯軸器 4) 部件軸承 5) 待測部件

6) 部件軸承 7) 圓柵尺 8) 光學尺軸

9) 部件軸

雖然全面介紹不同聯軸器設計的缺陷不在本文的討論範圍內，但需要考慮幾個重要因素：

反向間隙

旋轉驅動系統中的任何反向間隙都會導致所報告的角度位置隨旋轉方向發生變化，這對系統重複性的影響最為顯著。

抗扭剛度

聯軸器的剛度可能不如其所連接的軸，因此可能會受到振動/共振和軸扭曲的影響，如果該聯軸器用於反饋迴路，可能會顯著影響瞬態效能、穩定時間、容許的閉迴路增益和頻寬。

角度誤差

在某些校準條件下，大多數聯軸器會在傳動軸和從動軸之間引起角度誤差（例如，如果兩軸的軸線不平行，Oldhams 聯軸器會產生每轉 4 次的誤差）。對於高精度系統，旋轉光學尺應與待測部件牢固安裝在同一軸上，並在同一軸承上旋轉。

軸扭轉效應

待測部件與圓柵尺之間的軸如果缺乏抗扭剛度，將引起動態誤差，進而降低系統效能。為最大程度降低該效應，我們建議安裝非接觸式光學尺時，應使其盡可能靠近待測部件（見圖 6）。

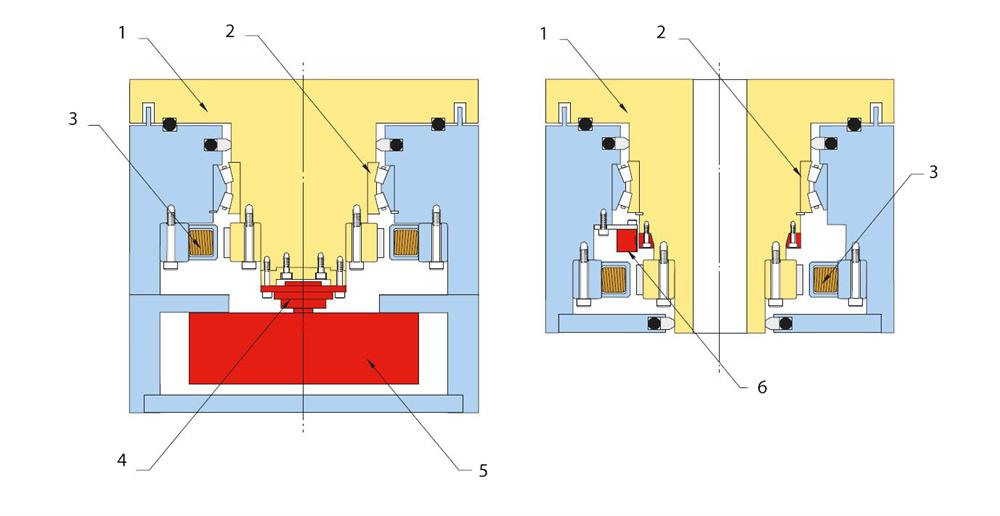
圖 6.封閉式光學尺和開放式旋轉光學尺。1) 軸 2) 軸承 3) 馬達 4) 聯軸器 5) 封閉式光學尺 6) RESM 旋轉光學尺

柵尺偏心和扭曲效應

準確量測角度最簡單的方法是，讀取與旋轉軸保持恆定距離的均勻線性刻度的計量尺規。完美旋轉柵尺偏心安裝引起的這些刻度標記的半徑變化會產生誤差，這些誤差每轉變化一次。柵尺扭曲會產生其他誤差，這些誤差每轉變化兩次或更多次。

以半徑為r₀ 的完美旋轉柵尺為例。柵尺的安裝使其以相位角 _Φ₁ 繞距離標稱柵尺中心 a<328>1</328> 處的某個點旋轉（見圖 7）。在任意方位角 _θ1，旋轉中心與柵尺表面的距離 R_θ 表示為：

R_θ = r₀ − a₁cos(_θ − Φ1)

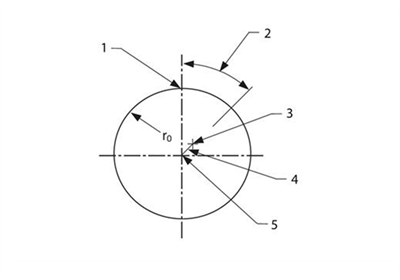
圖 7.當圓柵尺的旋轉中心偏離柵尺幾何中心時，會出現柵尺偏心誤差。

1) 標稱零方位 2) 相位角 Φ₁3) 旋轉中心

4) 偏心度 a₁5) 柵尺中心

因此，每旋轉一周，真實半徑將呈正弦變化，其幅度等於偏心度。

為了增加柵尺扭曲的效應，可以將旋轉光學尺的整體形狀視為一系列不同頻率n、相位 _Φn 和幅值 <350>a_n 的正弦波的總和，因而方位角 θ 的柵尺半徑表示為：

R_θ = r₀ − a₁cos(θ − Φ₁) − a₂cos(2θ − Φ₂) − a₃cos(3θ − Φ₃) − …….. − a_ncos(nθ − Φ_n )

可以看到，幅值 _a_n（均值至峰值）的正弦變化扭曲引起的最大圓周誤差E_n 如下所示，且每轉迴圈 n 次：

±E. = a_n/n

舉一個最簡單的例子，偏心度 1 µm（即 n = 1）將引起圓周正弦線性誤差 ±1 µm。

高階柵尺扭曲的幅度增幅將越來越小，對柵尺精度的影響也將越來越小。低次諧波會產生顯著影響：偏心度引起的誤差效應可能與軸承跳動的效應相似。

Renishaw 的旋轉光學尺安裝在錐面安裝座上時會出現少量的幾何變形，這可能表明，量測會受到偏心和扭曲，特別是由多個緊固螺栓和錐面安裝座引起的潛在各向異性效應的影響（如圖 8 所示）。然而，在一個標準安裝的 200 mm 旋轉光學尺上，使用 12 個擰緊到正確扭矩設置的螺栓進行固定時，不會引起明顯的誤差；每轉 12 個週期的誤差「噪音」約為 ±0.05 µm。

在典型安裝中，60% 或以上誤差由偏心（由於安裝）引起，低次諧波（主要是第 2 到第 4 次）產生的安裝誤差比例越來越小。幸運的是，偏心和扭曲引起的誤差可以用補償技術來應對，其中最有效的方法是使用多個讀頭。採用兩個讀頭可消除偏心和所有其他奇次諧波引起的誤差。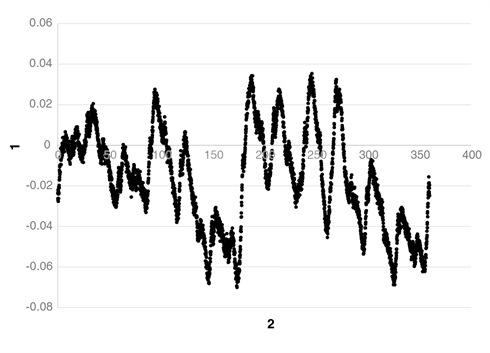

圖 8.旋轉光學尺的各向異性引起的每轉 12 個週期的誤差。

1) 位置誤差 (µm) 2) 旋轉角度 (⁰)

在某些安裝中採用四個讀頭可取得良好的效果，但增加更多的讀頭往往會逐漸降低投資回報：仔細選擇旋轉光學尺截面形式是限制高次失真諧波更有效的方法。

Renishaw 旋轉光學尺裝置採用了專利錐面安裝座，有效地將旋轉光學尺可能出現的偏心和扭曲轉變為幅度較小的偏擺，大大降低對精度的影響。例如，錐面安裝座將 200 mm 旋轉光學尺的 1 µm 偏心度轉變為偏擺幅度為 0.002° 的同心旋轉光學尺，從而提高量測精度，而無需使用多個讀頭。

柵尺偏擺的效應

偏擺是指旋轉光學尺與待測部件同心安裝，但其幾何軸向旋轉軸方向傾斜的情況（如圖 9 所示）。從側面觀察（即徑向），這種偏擺會使旋轉光學尺的圓周每轉一周發生一次正弦軸向運動。

偏擺具有兩種不同但細微的誤差機制。對於第一種機制，以直徑 200 mm 旋轉光學尺（帶有軸向刻度）為例，安裝時偏擺幅度為 0.1°。

安裝過程中，已經使用在柵尺表面上運行的千分錶 (DTI) 將柵尺調整為同心。在旋轉一周的過程中，不僅柵尺相對於讀頭軸向移動 ±0.175 mm，柵尺刻度的扭擺角也會在其標稱值的任一側 ±0.1° 的範圍內變化。如果將讀頭放在與 DTI 相同的位置（如圖 10 所示），則產生的誤差為二階。然而，如果讀頭從該點軸向位移 1 mm；軸向運動、扭擺角和讀頭位置變化相結合，將在圓周處引起每轉一次且呈正弦變化的約 ±1.74 µm 的誤差（±3.6 角秒）。

第二種機制是這樣的：從正面看，圓形硬幣呈圓形。如果在眼前偏擺這枚硬幣，則呈橢圓形。偏擺圓柵尺的影響與之相似，具有產生每轉兩次誤差的效應，該誤差的大小與偏擺角的余弦成反比。這是一種二階效應，在上述例子中，誤差為 ±0.16 角秒：就大多數應用而言，該誤差機制可以忽略不計。

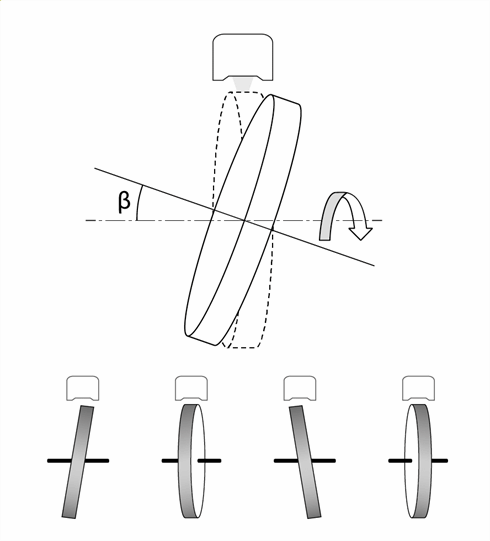
圖 9.當圓柵尺的幾何軸向旋轉軸傾斜時，會產生偏擺誤差。

讀頭引起誤差的效應

計量尺規只是光學尺系統的一部分，讀頭也會影響總體誤差預算。讀頭引起的最顯著的誤差如下：

細分誤差

具有 3,600 個刻度的旋轉光學尺，每 0.1° 或 360 角秒有一個刻度。如果所需的解析度比該柵距更精細，則需要讀頭具有細分功能。細分中的任何非線性因素將導致週期誤差，也稱為電子細分誤差 (SDE)。

以 Renishaw 讀頭為例，柵尺和讀頭指示光學尺產生的光學條紋隨著柵尺的運動橫向移動通過讀頭光電探測器。這些條紋的強度呈正弦變化，由讀頭解碼為兩個相位相差 90° 的正弦電壓。

如果在示波器上顯示這兩個相對電壓，會生成一個圓形利薩如圖形，每移動一個柵距該圖形就旋轉一次。如果該利薩如圖形是完美的圓形，並且以原點為中心，則其旋轉速度與柵尺的運動將完全一致；如果細分方法具有真正一致的角度分辨力，則讀頭細分是完美的，否則就會出現電子細分誤差 (SDE)。

電子細分誤差 (SDE) 受讀頭調整（與柵尺旋轉中心對準）、柵尺調整和柵尺清潔度影響：精心維護和謹慎安裝系統非常重要。讀頭的光學設計也決定了電子細分誤差 (SDE) 的效能：對於 Renishaw 的 20 µm 柵距 TONiC 系統，電子細分誤差通常為 ±30 nm（在 200 mm 旋轉光學尺上為 ±0.06 角秒）。

由於電子細分誤差 (SDE) 往往在高頻率下發生，補償幾乎無法消除電子細分誤差 (SDE) 的效應，但在小距離範圍內取平均值可能對某些應用有效。

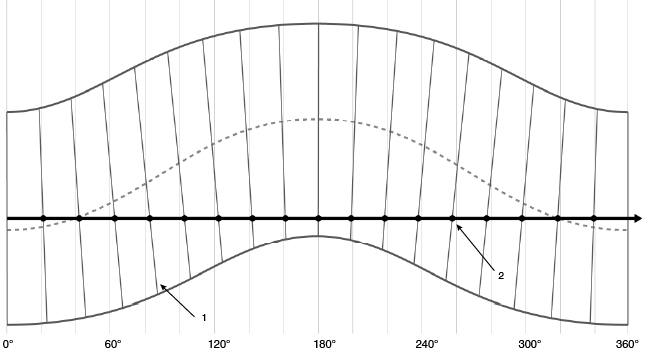
圖 10.偏擺效應導致柵尺隨旋轉角度振盪。粗黑線表示柵尺上的讀頭/DTI 位置，虛線標記柵尺中心線。黑點表示柵尺在讀頭下方旋轉時每個柵尺標記的視位元。

1) 柵尺標記 2) 柵尺上的讀頭位置

視差

如果柵尺與讀頭之間的距離發生變化（例如由於旋轉光學尺偏心、溫度變化等），除非讀頭與柵尺旋轉中心線正確校準，否則將引起誤差。如果讀頭發生俯仰，則間隙的變化將引起與俯仰角正弦成比例的量測誤差（如圖 11 所示）。

安裝穩定性

牢固、穩定地安裝讀頭對於精確和重複的角度量測極為重要。系統的設計應使讀頭不會隨著姿態、負載、溫度、振動等的變化而相對於柵尺旋轉軸移動。

如果系統產生意外較高的不可重複誤差，則有必要檢查以確保固定讀頭的螺栓，以及相關支架和安裝件沒有隨著時間推移而鬆動。

柵尺刻度精度的效應

在製造旋轉光學尺時，製造商會將刻度直接刻劃在基體上（而不是刻在線性尺上，然後再固定到圓盤或圓環的圓周）。製造商可將柵尺坯件固定在心軸上，然後旋轉心軸來確定每個刻度的位置。刻度刻劃完成後，將刻劃後的柵尺從心軸上取下之前，測得的柵尺精度（刻度的實際位置與預期位置之間的差異）被稱為「刻度誤差」。如果重複該量測，但這次使用正確調整的讀頭，則除刻度誤差外，誤差還包含讀頭引起的分量（主要是電子細分誤差 [SDE]）；該誤差稱為「系統誤差」。

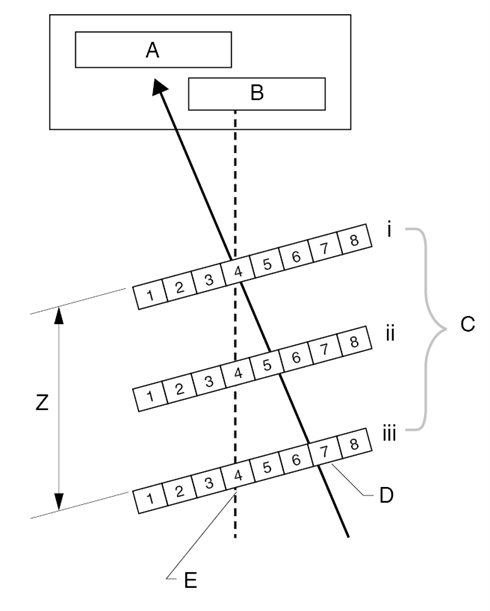
圖 11.視差是當柵尺（相對於讀頭）俯仰時，光學尺讀頭間隙改變導致的量測誤差。如圖所示，光源的光入射在柵尺位置 4 上，但隨著間隙的增加，探測器會讀取位置 5 和 6。

A) 探測器 B) 光源 C) 不同間隙 D) 探測器看到的視位 E) 柵尺上入射光束的實際位置

此時，如果取下旋轉光學尺並將其重新安裝在相同或不同的心軸上，並使用讀頭檢查其精度，所記錄的誤差又不同。該差異相當於旋轉光學尺初次安裝以進行刻度刻劃與重新安裝以進行使用之間的偏心度和高階不圓度變化引起的誤差。

本例中測得的總誤差稱為「安裝誤差」，該誤差定義最能反映使用者在現場實現的效能。

綜上所述：

刻度誤差 = 製造時進行刻度劃分的誤差。

系統誤差 = 刻度誤差 + 電子細分誤差 (SDE)

安裝誤差 = 系統誤差 + 安裝差異的效應

在典型安裝中，這些誤差大小往往不同；表 1 給出了對 Renishaw 大量直徑 200 mm 的旋轉光學尺進行測試的結果。直徑為 200 mm 時，1 微米對應 2.06 角秒。

誤差類型	Ø200 旋轉光學尺的典型誤差 (µm)	Ø200 旋轉光學尺的典型誤差角秒
刻度誤差	0.5	1.0
系統誤差	0.53	1.1
典型安裝誤差（1 個讀頭）	2.5	5.2
典型安裝誤差（2 個讀頭）	1.0	2.1

表 1 - Ø200 旋轉光學尺上總安裝誤差的組成因素。

刻度誤差和系統誤差由光學尺製造商定義，但額外的 ±2 µm 安裝誤差的責任由製造商和客戶共同擔負。即使客戶安裝的光學尺能夠確保完全同心並保持完美圓形，系統誤差和安裝誤差之間仍然存在差異（除非客戶將旋轉光學尺安裝在與製造商刻劃刻度時的安裝位置完全相同的位置）。

刻度誤差的產生取決於製造工藝：

對於通過在碟盤/旋轉光學尺邊緣周圍刻劃/蝕刻各個軸線而製成的旋轉光學尺，刻度誤差由刻度製作過程中產生的誤差引起。
對於採用掩模和蝕刻技術製成的徑向玻璃光學尺，刻度誤差由掩模精度誤差和蝕刻過程中掩模放置誤差共同引起。
對於將線性光學尺固定在既定軸的圓周上的旋轉光學尺系統，刻度誤差由線性光學尺的製造精度、線性光學尺的厚度及既定軸半徑的變化，以及將線性光學尺固定在軸上的張力差異引起。

準備階段結束後，最後一種刻度誤差可能會發生變化，因為溫度變化加上柵尺與軸之間熱膨脹係數的差異可能會導致柵尺相對於軸表面發生蠕變。如果用膠水來固定柵尺，則膠水鬆弛會增大此效應。

而 Renishaw 旋轉光學尺和碟盤，以及其他圓柵尺的刻度誤差不會隨時間變化，每次旋轉的刻度誤差均可預測，對於用戶來說，刻度誤差與安裝精度的效應無法區分；因此，可以使用相同的技術來降低誤差。

如果旋轉光學尺邊緣的軸向刻度發生偏轉或與旋轉軸線不完全校準，就會出現細微的刻度誤差。

這在純粹的旋轉運動期間沒有影響，但旋轉光學尺相對於讀頭的任何軸向運動（由於軸承中的軸端浮動）將錯誤指示柵尺旋轉。這種機制類似於前述的第三種偏擺機制。徑向柵尺所用讀頭俯仰不正確（即存在視差）的影響與之相似。

誤差補償技術

確定了運動控制系統所有誤差源的影響之後，可以對達到裝置技術規格所需的精度與未經補償的旋轉光學尺系統的預期效能進行比較。如果未經補償的旋轉光學尺系統無法達到所需的精度，則必須做出選擇：要麼選擇具有更高規格的不同光學尺系統（如果能夠找到可滿足安裝空間、交付期及預算要求的新光學尺），要麼運用誤差補償技術，以消除效能短板。最有效的兩種補償方法是使用多讀頭和誤差補償。

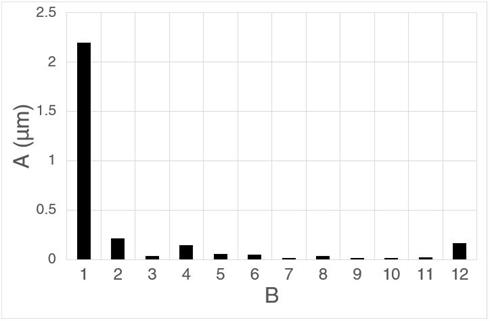
圖 12.旋轉光學尺誤差補償的快速傅立葉轉換；第一諧波對應旋轉光學尺偏心，是總安裝誤差的最大分量。

A) 誤差 B) 諧波

多讀頭

安裝兩個對徑讀頭，可以消除偏心效應以及重複性誤差的更高階奇次諧波。這種方法還可以消除角度量測時軸承跳動的效應，但消除軸承跳動以實現準確的極座標定位通常需要四個讀頭。增加所使用的讀頭數量將進一步減少重複性誤差，但一般認為安裝四個以上讀頭的複雜性和成本遠大於其優勢。這種多讀頭技術無需進行精心校準即可獲得效果；在時間和測試系統設計方面都具有很大的益處。

誤差補償

如果選用的控制系統組態為使用誤差補償，則可以用它來減少重複性誤差。為使該技術奏效，在最後組裝旋轉光學尺系統之後，必須由原始設備製造商使用干涉儀或其他經認可的量測基準對其進行校準。

安裝人員不能依賴光學尺製造商提供的任何校準證書，因為這會忽略安裝過程中引起的任何誤差，導致誤差補償毫無意義。優化誤差補償點的數量非常有利：對於正弦變化的週期誤差，每個週期補償七個點，可消除該頻率下約 90% 的誤差（如圖 12 所示）。因此，一百個點誤差補償可補正前十四個諧波中的大多數誤差，但應注意，這可能會增加由剩餘的更高次諧波引起的誤差。需要記住的是，該技術對軸承跳動、軸扭曲或其他時間相關的誤差源的效應沒有影響。

總結

本文簡要介紹了確定旋轉光學尺系統的實際規格時必須進行的一些權衡與取捨。此外還探討了一些限制可實現精度的更重要的因素，並詳細介紹了許多用於提高此可實現精度的技術。有關本主題的更多資訊，可參閱 ISO 230-7:2015（第 7 部分 – 旋轉軸的幾何精度）。

有關詳細產品資訊，請上：www.renishaw.com/encoder